Collaboration with: Dimitri Van De Ville, Thierry Blu, Torsten Möller, and Derek Bingham

In experimental design for computer simulations, points have to be chosen that determine the factor levels for the input variables for a certain number of experimental runs.

With such applications in mind and seeing further use for grid-based data processing in general, we propose novel sub-sampling schemes for lattices that allow for a small factor in the relative decrease of sample points between refined and coarse lattices that is independent of the dimension $d$ of the experimental region (i.e., the number of pre-screened, relevant input variables of the simulation code).

Our initial results were presented at SAMPTA 2009 with an extended discussion in Chapter 3 of my PhD thesis (PDF).

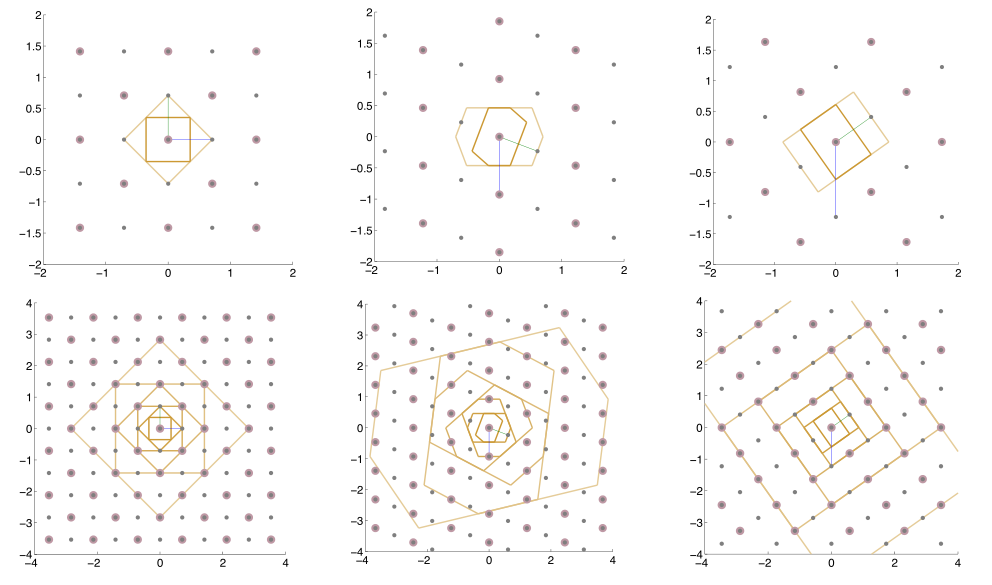
Each column shows a different lattice with several levels of refinement. The top row shows the refined lattice as small grey dots and the coarse sub-lattice is shown as thick dots. The Voronoi cells, or so-called nearest neighbour cells, for the two nested lattices are also shown. The bottom row shows the same lattices as in the top with additional levels of refinement and coarsening.

The special property of the nested lattice sequences we construct is that each lattice is a scaled and rotated version of the other lattices in the sequence. We show how to obtain low distance scaling factors, such as $2^{1/d}$ for any dimension $d$ resulting in changes of expected runsize by a factor as low as $2$ at each step in the sequence of nested experimental designs.

Currently, an extended discussion of this work with more recent applications is under preparation in collaboration with Derek Bingham.